Flagshift
Published on 16 Mar 2022
Description
We found a weird logic circuit called Flagshifter that could theoretically generate new flags. We don’t fully understand it yet, and would take a long time to look through it by hand, so it would be great if you could write a simulation program to see if we can find something interesting in the output.
- Author: gb
- Attachments: challenge.png
Solution
We are given the following image and the task seems simple: implement the logic, and you get the flag.
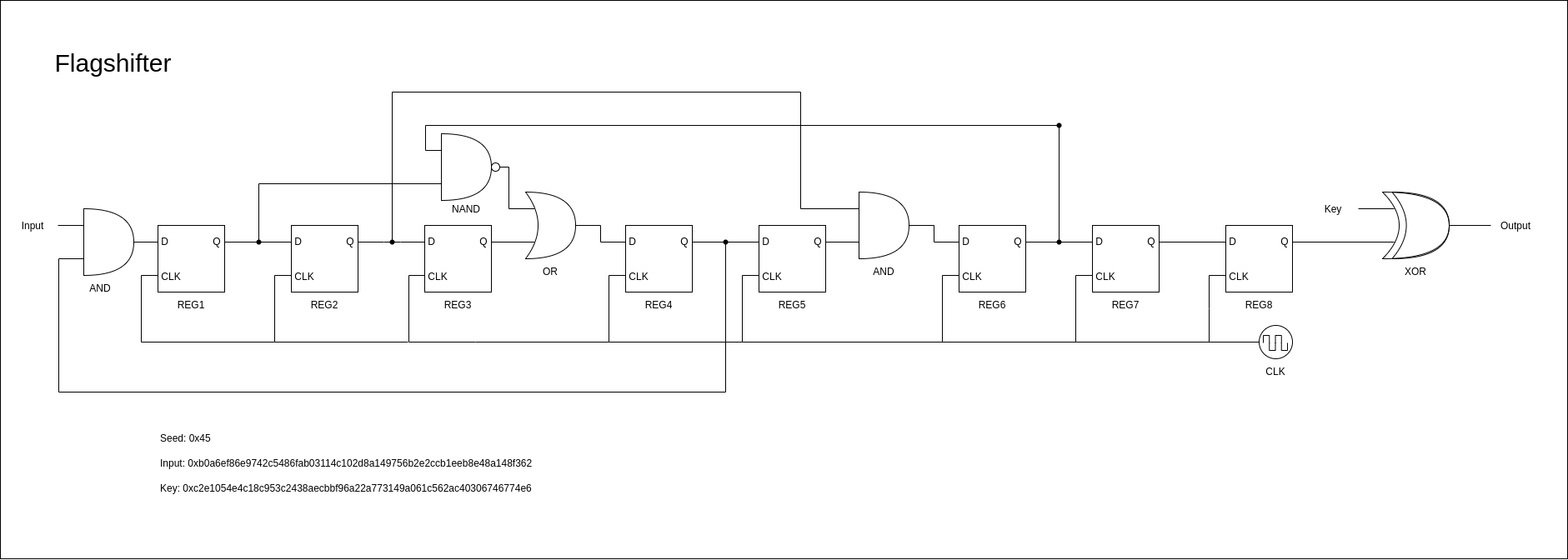
I chose to implement the logic in python, and for sake of simple coding, kept everything in binary data form, so I don’t have to convert in the code, just do the conversion once using CyberChef.
def NAND(n, m):
return int(not (n & m))
def OR(n, m):
return n | m
def AND(n, m):
return n & m
def XOR(n, m):
return n ^ m
inp = "10110000101001101110111110000110111010010111010000101100010101001000011011111010101100000011000100010100110000010000001011011000101000010100100101110101011010110010111000101100110010110001111011101011100011100100100010100001010010001111001101100010"
key = "11000010111000010000010101001110010011000001100011001001010100111100001001000011100010101110110010111011111110010110101000100010101001110111001100010100100110100000011000011100010101100010101011000100000000110000011001110100011001110111010011100110"
r1 = 0
r2 = 1
r3 = 0
r4 = 0
r5 = 0
r6 = 1
r7 = 0
r8 = 1
out = ""
for i in range(len(inp)):
r1o = r1
r2o = r2
r3o = r3
r4o = r4
r5o = r5
r6o = r6
r7o = r7
r8o = r8
r1 = AND(int(inp[i]), r4o)
r2 = r1o
r3 = r2o
r4 = OR(r3o, NAND(r1o, r6o))
r5 = r4o
r6 = AND(r5o, r2o)
r7 = r6o
r8 = r7o
output = XOR(int(key[i]), r8o)
out += str(output)
print(out)
The acquired flag is:
cd22{HIDDEN}